2D imaging analysis: parametric method
Parametric methods used particular functional forms to fit two-dimensional galaxy light distribution. It has the advantage that extrapolating flux at large radii reasonably well, better separating the overlapping components, and accounting for the PSF effect. Therefore, parametric methods provide robust determination of galaxy sizes and luminosities, as well as substructure properties. While non-parametric methods are model independent, its main disadvantages are that they are sensitive to the image depth (i.e., S/N), because there is no parametric form for extrapolating to account for the faint outer parts of galaxies, one can underestimate flux and size for faint galaxies. The main weaknesses for parametric methods are generally computationally intensive (such as the bulge-disc decomposition) and are subject to parameter degeneracy. They also assume that analytic profiles can perfectly describe the real galaxies. \(\)$$ \Sigma (r) = \Sigma_{ \rm e}\ $$
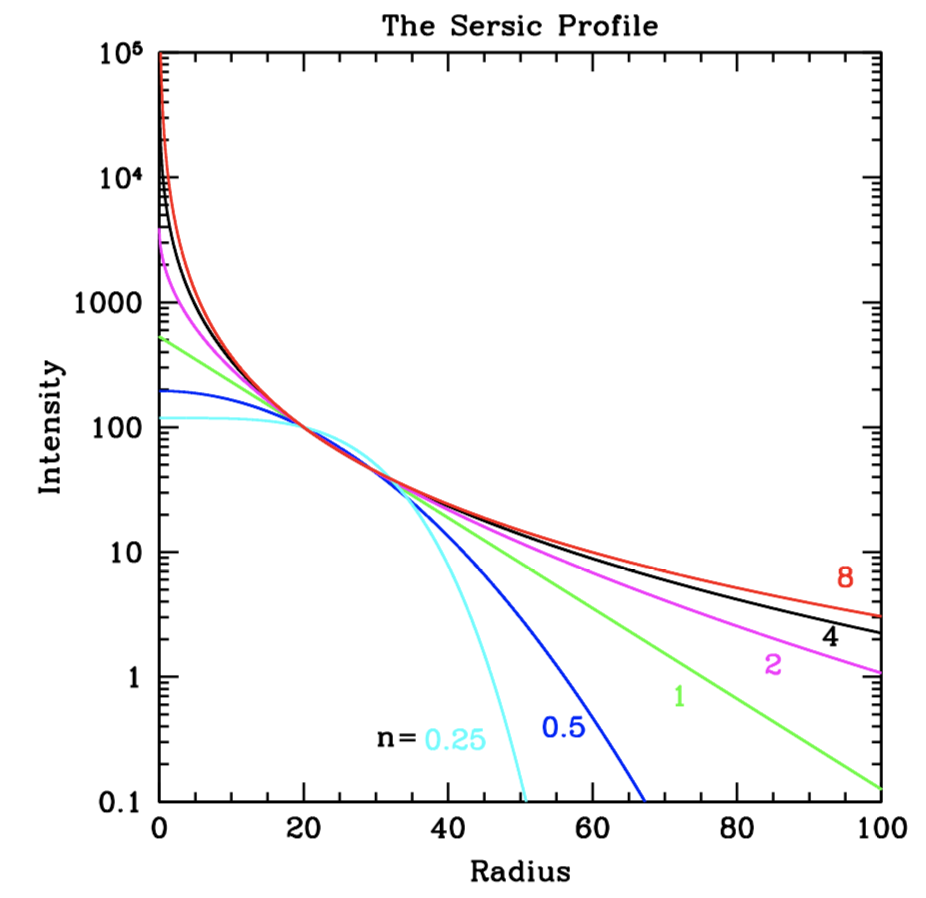
Sérsic profile (Sérsic 1963, 1968) is the most general and flexible analytic profile to model the radial surface brightness distribution of a galaxy. Fitting the entire galaxy with one Sérsic profile has become standard practice in the literature, particularly for observations with limited depth and spatial resolution that prohibit more complex modeling. In large galaxy survey, single-component Sérsic fitting is a fundamental way to robustly determine the integrated properties of a galaxies (such as mag and Re), especially for crowded galaxy fields where blending effects become severe. The Sérsic profile has the following functional form:
\(\)$$ \Sigma (r) = \Sigma_{ \rm e}\ $$
\(\)$$ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$
发表回复